Fibonacci Meets Pythagoras...

Here is an interesting pattern I found while substituting Fibonacci Numbers into the primitive solution for the Pythagorean problem.   The primitive solution to the Pythagorean problem is:

a² + b²= c²  
Given any two arbitrary integers  m  and   n 
 a =  n²  -  m²
 b =  2mn
 c =  m²  +  n²



I am not providing a full proof of this solution here. I am simply showing the solution because I use the solution to generate some very interesting patterns. I used Fibonacci numbers in the primitive solution and got the following results.... ↓ ↓ ↓ ↓ ↓ ↓ ↓


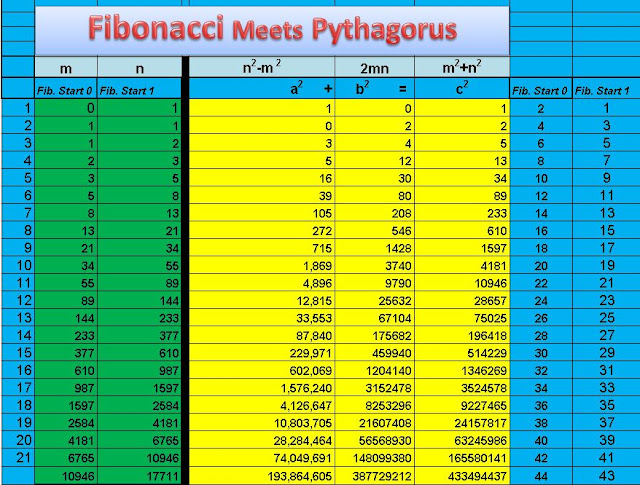
  Some of the Pythagorean triples from the chart are:
   3²  +  4² = 5²
  5²  + 12² = 13²    Look at the c terms do you see a pattern?.......                                                                  16² + 30² = 34²     That's right the c terms are all Fibonacci numbers.                                                          39² + 80² = 89²                                                                                       
                                                                                                                 
               If you look in the columns under the  m and the n you will notice that I have the Fibonacci sequence written in two ways the m column I started the Fibonacci sequence with 0 which still works with the pattern, and in the n column I have the Fibonacci sequence starting with 1.  I do this so when I substitute the numbers into the primitive Pythagorean solution They wont just zero out.


         There is also another interesting pattern I found with the Fibonacci/Pythagorean triples.  
If you look in the two columns on the right I have showed the place value the c terms are in the Fibonacci sequence. Example: the number 1 is the 2nd  number in the Fibonacci sequence and the number 2 is the 4th. And this is their place value when you start the Fibonacci sequence with 0.Using the column where I started the Fibonacci sequence  with 1 the corresponding c terms are in the odd place values instead.

To explain it another way here I will list out a few of the numbers from the c column

1. 1   is the 2nd Fibonacci number when the sequence starts with 0 and the 1st when it starts with 1
2. 2    is the 4th Fibonacci number when the sequence starts with 0 and the 3rd when it starts with 1
3. 5      is the 6th Fibonacci number when the sequence starts with 0 and the 5th when it starts with 1
4. 13    is the 8th Fibonacci number when the sequence starts with 0 and the 7th when it starts with 1
5. 34    is the 10th Fibonacci number when the sequence starts with 0 and the 9th when it starts with 1
6. 89  is the 12th Fibonacci number when the sequence starts with 0 and the 11th when it starts with 1
7. 233 is the 14th Fibonacci number when the sequence starts with 0 and the 15th when it starts with1 

I could probably explain this better,but in general most should be able to look at the chart and see the patterns.  There is also more patterns found here when doing this.  The one I like is the c column has a lot of prime numbers. a few of them are     2,    5,   13,  89,    233,    1,597,   28,657.
 I have carried this out as far as Excel will let me without throwing errors and all of the c terms are Fibonacci Numbers
I am curious to see what patterns the rest of you come up with.     Happy Hunting!!!!!!!!!!