With the recent changes made to the pell grant eligibility rules, many low income students are left with basically two options. Dropout , or go deeper into debt by attempting to get more student loans. The changes to the pell grant were intended to save money in the budget by cutting education spending, and to eliminate the students who "abuse" the system. The main target being students who have spent six years attempting a bachelors or associates degree. However, with the way the law is setup is on percentage meaning that institutions or students that do not follow a "traditional" schedule will be cut off after just three years in some cases.
On a personal note, my wife is one of these affected students. She works full time and goes to school full time. When she first applied for the pell grant 3 years ago she was ensured to get through a 4 year bachelors program. Here we are 3 years later, and in the middle of a semester she is informed by the financial aid dept she needs to come up with $2000 to just finish the current classes she is in. This has put a great strain on our family. Now we are both going to have to work full time and hope that after paying for child care and bills there is enough left over to pay a fraction of the educational cost. If we were to save the money to cover the costs she would still have to take several months in between classes just to save enough for the next class. This will make her Aug 2013 graduation date be pushed far into 2014(if not beyond).
The situation for my wife is not an uncommon situation people are facing. There is a large number of students face similar circumstances. We have seen so much in the media about a growing need for qualified workers in the workforce. With these changes the media byline needs to be modified to "There is a growing need for middle to upper class qualified workers" The lower class has been effectively eliminated from the "qualified workers" category. So what message is our government sending us? Lower class shall remain lower class and barring a streak of extremely good luck, will never be able to crawl their way out. To most lower class families the middle and upper class is like an elite club that you can only be a member of if you have the right last name, win the lottery, or were lucky enough to get a "better than minimum wage" job.
Sorry for the rant, but I feel this was a very dangerous move on the part of the government. The number of dropouts and student loan defaults could potentially double if this is not amended. It represents a "huge" over site as to the problems this is going to cause and the damage it is going to do to the economy and the future workforce as a whole. A simple fix could be just adding a clause to the rule that allows students who are within a year from graduation to continue to receive funds until their reasonably anticipated graduation date, and if they do not complete their degree by that time then a cutoff of funds is reasonable. For students who already have a bachelors degree should be the ones with more strict cutoff schedules for funding a second bachelors or associates.
Monday, October 29, 2012
Friday, September 21, 2012
Computer Programming and Mathematics
Computers and Mathematics
As some of you may already know,there is a significant relationship between Mathematics and Computer Programming. Many mathematicians use programming to aid in their research. It can be an invaluable tool to achieving success in whatever proof you may be working on. My interest in how they connect is the algorithms you must create to apply to your program. In order to utilize a computer program to aid you in mathematics you must first write an algorithm,assuming you already know the programming language you will be using. The algorithm must then be translated to work in the programming language you chose.
Prime Number Checking
One of the most basic programming solutions is writing a program to find out if a given number is a prime number. The first step is to develop your algorithm. There are many different ways to check the if a number is prime or not. Most of them fairly complex, however there is one very simple technique. A prime number is only evenly divisible by one and itself. So the easiest way is to use modular division, which is simply dividing two numbers and keeping only the remainder. For example 32 modulo 5 = 2,
because 5 goes into 32, 6 times with a remainder of 2. Since prime numbers are only evenly divisible by one and themselves, prime numbers would always have a remainder greater than 0 when divided by all other numbers(other than 1 and themselves). With this knowledge we know that we have to test all numbers between one and the number we want to check if its prime.This can be limited even further by adding that the factors on any number can not exceed the square root of that number. Now our plain language algorithm is :
get number and call it n
calculate square root of n
test all numbers >=2 and <= square root of n
and if none of the numbers tested return a 0 remainder the number is prime
Java code to find if a number is prime
Our next step is to translate our algorithm into computer code. I will use java because that's my favorite so far. If you are not familiar with java you can find out more at http://docs.oracle.com/javase/tutorial/getStarted/index.html
The part of our algorithm where we calculate the square root and test all the numbers up to the square root is best achieved by a for() loop.the variable we will use to represent the number we want to test will be n and we will make it a "double" data type we will be using double for two reasons one the included Math.sqrt method we will be calling requires a double,.and the second reason is that we can check much higher numbers with double.The next variable we want will be used to store the numbers we are using in our modular division we will call it k and make it a double
lets code out our for() loop
double n;
double k;
for(double k = 2;i<=Math.sqrt(n);k++){
if(n%k == 0){
return false;
}
} return true;
That is our complete algorithm for prime checking translated into Java. I have tested this algorithm for numbers up to 500 digits long before it started to slow my pc. which is a few years old. I will gladly answer any question or comments on how to implement this into your java project as well as put more posts with how to make other java programs related to mathematics. Just leave a comment with you questions, requests, or suggestions . Thank you for stopping by.
Labels:
math and technology,
number systems,
Silicon Valley
Wednesday, April 18, 2012
Open book learning versus rote learning
What
is rote learning?
Rote learning is the concept that
you will memorize a procedure by endlessly repeating it until you “understand”
it. Some believe this is the only way to
truly understand a topic in mathematics.
It is the “practice makes perfect” paradigm. The rote learning idea is that understanding
is derived from memorization and recall over time. [edit:(9-24-2015) As we learn more about the human brain and the way it carves and hones pathways, we begin to see the the role of rote learning. We have come to learn that rote memorization of key concepts tends to in a way free up "ram" ,working memory, in our brains. With key concepts being stored in long term memory, our brains are able to process higher level logic faster. ] Understanding means to
comprehend or to grasp the meaning of. Students with good memories will just
simply memorize the formulas and recall them on demand at test time, and the
teacher will believe they understand the concept and move on. Students who do not have great memories will struggle
and get frustrated while trying to memorize the formulas. We can single them
out in an attempt to give them extra help to understand, which in some cases actually
embarrasses the students. [edit:(9-24-2015) A strategy to overcome singling out students with poor memory, is to implement a small section on memorization techniques. Proper application of memorization strategies can also teach concentration and focus techniques. (link 'www.psychologytoday.com')]
Embarrassment even in the smallest amount
begins a psychological impairment on a child’s ability to learn. No matter how
we approach the situation singling out one student or even multiple students
can impair learning. Now I am sure there
are some very exceptional teachers with the amazing ability to approach a
student to find out why they are failing with minimal impact. Unfortunately,
not all teachers can do this; it is a talent of charisma that we just simply cannot
teach everyone. We are now left with the question: How do we give the children
that need this extra attention help without singling them out? We first need to
remove the extra pressure of rote learning exercises. We can do this by
utilizing Open book learning approaches.
What
is open book learning?
Open book learning takes away the
pressure of having to cram for a test. Relieving a student’s stress will create
a better atmosphere of learning. In introductory courses, having a system based
on pure open book examinations can cause some problems of students not studying
or reading the material before the test. To alleviate this problem you can
implement both open book and closed book exams.
The exams need to be structure for whether it is open book or not. For
the open book tests do not put in direct information that can be simply copied.
Present the questions where the students will have to apply the knowledge
rather than recall or look them up and simply copy it from the book. Keep it
random as well don’t let the students know what kind of test they are going to
be having, so you don’t discourage study.
Don’t
be one sided.
Stay flexible and implement all of
these strategies together. The mechanical rote learning approaches should stay
limited to introductory courses. Rote learning should never be the pass/ fail in
math education. A final examination
should be on concepts and understanding not recall of facts that anyone can
look up.
The purpose of education is career
preparation.[edit:(9-24-2015) The purpose of education goes far beyond career preparation. It is the cornerstone of human development and understanding our world. While career preparation is a tangible by-product of education, it is not the 'sole' purpose.] An engineer can still build
a great bridge even if they have to look up a formula. However; if they don’t
have a conceptual understanding of what to look up or how to look it up they won’t
be an engineer for long.
Sunday, April 1, 2012
Some Mathematical FACTS about poverty in the U.S.
According to the
Dept of health and human services, the poverty threshold in the U.S is as
follows.
|
2012 Poverty
Guidelines for the
48 Contiguous States and the District of Columbia |
|
|
Persons in
family/household |
Poverty guideline
|
|
1
|
$11,170
|
|
2
|
15,130
|
|
3
|
19,090
|
|
4
|
23,050
|
|
5
|
27,010
|
|
6
|
30,970
|
|
7
|
34,930
|
|
8
|
38,890
|
|
For
families/households with more than 8 persons,
add $3,960 for each additional person. |
|
Above Chart from http://aspe.hhs.gov/poverty/12fedreg.shtml
LET'S DO THE MATH
Let’s break this down a little bit. For the family of 3 the chart indicates that
to be considered in poverty you have to make less than $19,090 annually. The National
housing Conference gives the fair market average price of rent on a 2
bedroom as $960 monthly which is $11,520 annually. The U.S.
dept. of Agriculture gives the cost of food for a family of 3 as $439 monthly which is $5,268 annually. The average cost of utilities
(natural gas, water, electricity) varies widely but sits around $250 monthly
for most families. This is $3,000 annually.
Now to add all of this data up we get a base cost of $19,788 that puts us close to the
poverty threshold. This base cost does
not include
Average fuel costs as reported by CNN
are about $368 monthly which adds
another $4,416 to the annual cost of living. Our total is now $24,204 annually
Let’s stop at this number for now and see how it compares to
wages. The current minimum wage is
$7.25/hour At 40 hours a week that is $290.00 weekly( $15,080 annually before
taxes) Now if both parents were to be
working 40 hours a week we double this to get $30,160 before taxes.(this puts you above the poverty level and makes
public assistance unavailable) Now this is $5,956 more than the annual cost we have above, but with this
situation we have a new problem(child care) Which makes a new expense.
USA
TODAY reports that child day care ranges from $3,803 to $13,480 annually, for those lucky enough to live in an
area on the low average that will still leave you with $2,153 a year. However we are talking about a family of 3 here with
a child. Nowhere in our expenses did we include the other basics such as clothing
and toys(yes toys they are essential for a child’s cognitive development)
If your child is in diapers and you shop wisely you will
spend around $30 a week $1,560
annually on diapers (this number can vary slightly depending on special needs… sensitive
skin allergies etc. ) Subtract this
from the $2,153 we had left above we are now down to $593 However, with diapers we also need diaper wipes. A person
could bargain shop and get away with around $12 month on those. That is only
$144 annually, and when subtracted from $593 leaves us with $449 clothes, shoes, toys etc….
Another expense I left out is motor vehicle insurance which
is now a legal requirement in most states. The average costs varies greatly but
is around $1,500 annually leaving our money left over -$1051 There
are more expenses that are “necessary expenses” That I have not included, but
the fact remains It is impossible to live on minimum wage with a family of 3
and both parents working full time. This is why many people get caught up in
major credit card debt, have poor credit and stay in a cycle of survival by
destroying their financial future. Bad credit means higher interest and high
payments on any loan they try to get, which keeps them always broke. .
For those that do manage to survive by whatever means they
can are on a slippery slope. One emergency (car problems, health issues
preventing work, cut in hours etc…) can completely devastate a family living
off minimum wage.
Saturday, March 10, 2012
What math means to me?
I love math, but I
also realize that not everyone looks at math the same way. When I look at math,
I see the beautiful mystery that can define everything in our world and beyond.
I see a glimpse into unlocking the mysteries of the universe. Once you begin to
delve deeper into mathematics, you begin to have an understanding of the world
around you that only mathematicians get to enjoy.
After you have
gotten into to higher level mathematics, some of the problems you solve will
begin to fill up your page like a poetry of numbers. I know when I am solving problems that
fill up a page I will take my finished product and just step back and look at
the beauty of it. Even if you don't see the beauty in a page full of formulas, computers have allowed us to manifest formulas into beautiful works of art. Fractals offer us an in depth look at the artistic capabilities of even the most mechanical of ideas.
The connection math has to all other subjects is infinite. Even the art world uses mathematics. The golden ratio, related to Fibonacci numbers, is considered the formula for beauty. All of these various connections in mathematics further enhances the beauty it holds.
In addition to the art and poetry of mathematics, there is also the critical thinking aspect. Mathematics is logic conceptualized. It is about modeling our world into tangible coherent forms, and finding patterns and connections. Some refer to mathematics as the language of the universe, but it is beyond that. It is how we take abstract ideas and create a language to share and understand those ideas.
The connection math has to all other subjects is infinite. Even the art world uses mathematics. The golden ratio, related to Fibonacci numbers, is considered the formula for beauty. All of these various connections in mathematics further enhances the beauty it holds.
In addition to the art and poetry of mathematics, there is also the critical thinking aspect. Mathematics is logic conceptualized. It is about modeling our world into tangible coherent forms, and finding patterns and connections. Some refer to mathematics as the language of the universe, but it is beyond that. It is how we take abstract ideas and create a language to share and understand those ideas.
I know that most people do not look at math the way I do,
and I am interested in getting some feedback on What math means to you? Everyone
has their own story or way of looking at math, even if you are completely
frustrated with math I would like to see the comments I get.
So please leave some comments on what math means to you so
we can discuss and compare how everyone looks at it. I am very interested to
see the variety of responses I get.
Wednesday, February 22, 2012
An interesting pattern with derivatives
I found an interesting pattern while finding higher order derivatives using the power rule. For readers who are not familiar with derivatives you might want to watch the video here ( MIT open course ware derivatives.)
I was curious what the 3rd derivative of x5 was.
So I used the power rule to find the first derivative and I got f1(x)= 5x4 I applied the rule again to get the second derivative and got f2(x)= 20x3 I once again used the power rule for the third derivative and found the third derivative was f3(x) = 60x2 Now by this time I started to get curious as to what the Nth derivative,fn(x) would be for functions using the power rule. So I began to to work it out algebraically. I started with the general function f(x)= xa and began taking the derivative by continuously using the power rule, and got the following results:
Now with the a in the exponent xa we see that the a reduces by the the derivative we are on for example the second derivative , f2(x), the exponent is x a-2 That makes the general form for the exponent x a-n
To put all this together we get the formula for the nth derivative using the power rule as
f n(x)= a!/(a-n)! x a-n
I am not sure if this pattern was already discovered by someone else or not. I have done some research and have not been able to find anything about it online.
I was curious what the 3rd derivative of x5 was.
So I used the power rule to find the first derivative and I got f1(x)= 5x4 I applied the rule again to get the second derivative and got f2(x)= 20x3 I once again used the power rule for the third derivative and found the third derivative was f3(x) = 60x2 Now by this time I started to get curious as to what the Nth derivative,fn(x) would be for functions using the power rule. So I began to to work it out algebraically. I started with the general function f(x)= xa and began taking the derivative by continuously using the power rule, and got the following results:
- f 1(x)= a x a-1
- f 2(x)= a (a-1) x a-2
- f 3(x)= a (a-1)(a-2) x a-3
- f 4(x)= a (a-1)(a-2)(a-3) x a-4
- f 5(x)= a (a-1)(a-2)(a-3)(a-4) x a-5
- a
- a (a-1)
- a (a-1)(a-2)
- a (a-1)(a-2)(a-3)
- a (a-1)(a-2)(a-3)(a-4)
Now with the a in the exponent xa we see that the a reduces by the the derivative we are on for example the second derivative , f2(x), the exponent is x a-2 That makes the general form for the exponent x a-n
To put all this together we get the formula for the nth derivative using the power rule as
f n(x)= a!/(a-n)! x a-n
I am not sure if this pattern was already discovered by someone else or not. I have done some research and have not been able to find anything about it online.
Tuesday, February 21, 2012
Number Theory: Not as Scary as it Sounds
What is Number Theory?
Number
theory is simply the study of the properties of numbers. The topics in number
theory range from a variety of fairly simple to extremely complex. (Most people
can understand and follow along with topics in the middle of this range.) The
simplest properties of numbers are still a topic of research in number theory
today. A person can start becoming an amateur number theorist by simply picking
a number and finding all of the ways that number can be mathematically
manipulated. Then by paying attention to and recording any patterns that arise to see what new math tools you discover. While
doing this you can do a little research to find other ways to manipulate the numbers
you chose, and through the induction/deduction process of logic find your own
theories. You might not find anything groundbreaking, but you will certainly
find fun ways to learn and enjoy math on your own. I found an interesting “shortcut
for multiplying by the number nine by simply making a chart of all of the
multiples of nine and analyzed it until I found a pattern. I am not sure if
someone else has already found this or not, but it was a very fun “trick” to
use. You can find a full explanation with examples here Multiplying
by 9,99,999...etc
In high
school, you were taught some of the basic properties of multiplication. Such as: the distributive property, and the associative property. You were most likely
shown a formula to explain these similar to
a(b+c) = ab+bc, Which describes the distributive property.
a(b+c) = ab+bc, Which describes the distributive property.
Well where did we get this? It is simply a result of number theory, or
another way to define it is the logic of numbers. It is difficult to tell who
to actually give credit to for discovering this property; it is one of the most
widely used properties in mathematics. It
was, however; discovered by analyzing the properties and patterns found when
multiplying and dividing numbers. The use of the letters, or variables, comes
from what is called abstraction. Abstraction is simply taking something out of
its original context and making a general form of it. This is not a great definition,
but hopefully you see that when we find a pattern that is very useful, we need
to make a method to apply it to all numbers.
Now some may understand the
distributive property better if it is shown with actual numbers. Like this
2(3+4) = 2x3 + 2x4 but without abstraction some people would look
at the example using numbers and think it only applies to those numbers. Effective abstraction leads into using proofs
to check your pattern to see if it applies to all numbers or just a certain set
of numbers of numbers with specific properties.
I will leave that discussion for another post. Hopefully, this will give
you a basic understanding of what number theory is and inspire you to learn
more.
Monday, February 20, 2012
Create inspiration to learn math.
One
thing the current math education policies do not address is relieving math
anxiety. Many educators and policy makers talk about it, but do they really
have a solid plan for relieving it. The
common discussion is all about how math is taught, but what about the kind of
math that is taught. Some educators are
already implementing styles of teaching that relates to what students are
interested in. This is a step in the right direction, and this does increase an
interest in math education. Many
educators and even individuals have taken to the internet to provide lessons, practice,
discussion boards on math education and homework. When you look at all of these
education sites they all mostly just reflect the same things we teach in
schools.
Does this inspire students to learn
mathematics? Does this relieve math anxiety? One way to answer these questions
is to look at the students that are actively participating in these. Are they
doing better on tests? Maybe… We might
be improving scores in the small groups that are actively participating in
these online programs, but once again we have the question, are we relieving
math anxiety? Maybe to a small degree..
A simple way to relieve math
anxiety is to introduce students to simple math “tricks”, or other ways to
simplify or shorten the math calculations that most people only know one way to
do. I have already presented a couple of
these methods. Such as Long multiplication in Reverse also called left to right
multiplication, or multiplication without carrying. The “left-to-right” method
is a good trick which helps with mental math. Students can learn to answer more difficult
multiplication problems in their head with relative ease.
This
will make them more confident in their math skills. It will also change the way
their peers look at them. They will feel smarter and it will increase their desire
to be smarter by learning more about math. The “left-to-right” method is not the only “trick”
to make multiplication easy. There is also Russian Multiplication also known as binary multiplication. This method
is great because you don’t have to have the multiplication table memorized to
use it. You just simply have to double numbers and cut numbers in half and then
add.
All of these simple methods make
math easier to students, relieving their initial anxiety. With the many ways
that we can use to make math easier, we can teach a new “trick” every day. The whole point is to increase desire for learning
and relieve math anxiety. These are the
two main obstacles in helping children not only have better understanding of math,
but also to do better on tests.
Labels:
math teachers,
Mathematics Education,
shortcuts
Friday, February 17, 2012
Fibonacci Meets Pythagoras...
Here is an interesting pattern I found while substituting Fibonacci Numbers into the primitive solution for the Pythagorean problem. The primitive solution to the Pythagorean problem is:
a2 + b2= c2
Given any two arbitrary integers m and n
a = n2 - m2
b = 2mn
c = m2 + n2
I am not providing a full proof of this solution here. I am simply showing the solution because I use the solution to generate some very interesting patterns. I used Fibonacci numbers in the primitive solution and got the following results.... ↓ ↓ ↓ ↓ ↓ ↓ ↓
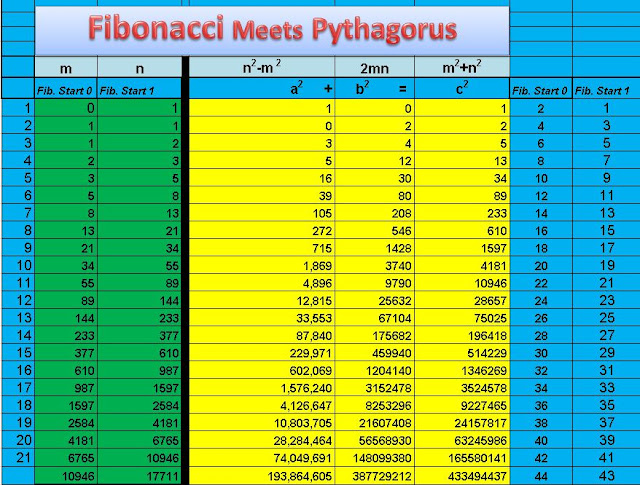
Some of the Pythagorean triples from the chart are:
32 + 42 = 52
52 + 122 = 132 Look at the c terms do you see a pattern?....... 162 + 302 = 342 That's right the c terms are all Fibonacci numbers. 392 + 802 = 892
If you look in the columns under the m and the n you will notice that I have the Fibonacci sequence written in two ways the m column I started the Fibonacci sequence with 0 which still works with the pattern, and in the n column I have the Fibonacci sequence starting with 1. I do this so when I substitute the numbers into the primitive Pythagorean solution They wont just zero out.
There is also another interesting pattern I found with the Fibonacci/Pythagorean triples.
If you look in the two columns on the right I have showed the place value the c terms are in the Fibonacci sequence. Example: the number 1 is the 2nd number in the Fibonacci sequence and the number 2 is the 4th. And this is their place value when you start the Fibonacci sequence with 0.Using the column where I started the Fibonacci sequence with 1 the corresponding c terms are in the odd place values instead.
To explain it another way here I will list out a few of the numbers from the c column
I could probably explain this better,but in general most should be able to look at the chart and see the patterns. There is also more patterns found here when doing this. The one I like is the c column has a lot of prime numbers. a few of them are 2, 5, 13, 89, 233, 1,597, 28,657.
I have carried this out as far as Excel will let me without throwing errors and all of the c terms are Fibonacci Numbers
I am curious to see what patterns the rest of you come up with. Happy Hunting!!!!!!!!!!
a2 + b2= c2
Given any two arbitrary integers m and n
a = n2 - m2
b = 2mn
c = m2 + n2
I am not providing a full proof of this solution here. I am simply showing the solution because I use the solution to generate some very interesting patterns. I used Fibonacci numbers in the primitive solution and got the following results.... ↓ ↓ ↓ ↓ ↓ ↓ ↓

Some of the Pythagorean triples from the chart are:
32 + 42 = 52
52 + 122 = 132 Look at the c terms do you see a pattern?....... 162 + 302 = 342 That's right the c terms are all Fibonacci numbers. 392 + 802 = 892
If you look in the columns under the m and the n you will notice that I have the Fibonacci sequence written in two ways the m column I started the Fibonacci sequence with 0 which still works with the pattern, and in the n column I have the Fibonacci sequence starting with 1. I do this so when I substitute the numbers into the primitive Pythagorean solution They wont just zero out.
There is also another interesting pattern I found with the Fibonacci/Pythagorean triples.
If you look in the two columns on the right I have showed the place value the c terms are in the Fibonacci sequence. Example: the number 1 is the 2nd number in the Fibonacci sequence and the number 2 is the 4th. And this is their place value when you start the Fibonacci sequence with 0.Using the column where I started the Fibonacci sequence with 1 the corresponding c terms are in the odd place values instead.
To explain it another way here I will list out a few of the numbers from the c column
- 1 is the 2nd Fibonacci number when the sequence starts with 0 and the 1st when it starts with 1
- 2 is the 4th Fibonacci number when the sequence starts with 0 and the 3rd when it starts with 1
- 5 is the 6th Fibonacci number when the sequence starts with 0 and the 5th when it starts with 1
- 13 is the 8th Fibonacci number when the sequence starts with 0 and the 7th when it starts with 1
- 34 is the 10th Fibonacci number when the sequence starts with 0 and the 9th when it starts with 1
- 89 is the 12th Fibonacci number when the sequence starts with 0 and the 11th when it starts with 1
- 233 is the 14th Fibonacci number when the sequence starts with 0 and the 15th when it starts with1
I could probably explain this better,but in general most should be able to look at the chart and see the patterns. There is also more patterns found here when doing this. The one I like is the c column has a lot of prime numbers. a few of them are 2, 5, 13, 89, 233, 1,597, 28,657.
I have carried this out as far as Excel will let me without throwing errors and all of the c terms are Fibonacci Numbers
I am curious to see what patterns the rest of you come up with. Happy Hunting!!!!!!!!!!
Labels:
Fibonacci,
patterns,
Pythagoras,
Pythagorean theorem,
sequence
Wednesday, February 15, 2012
Mathematics education in the technological age
There has been a lot of buzz about Silicon Valley’s role in mathematics education. Computers and the Internet have provided a
new outlet for people to share their knowledge.
You can find thousands of videos on nearly every subject on youtube. Surprisingly, many of these videos are
actually very informative. There are many
people out there with a significant amount of knowledge on the subjects they
discuss in their videos. Not all of them
are educators; many of them are normal everyday people who simply have a
passion and understanding for a particular subject. Mathematics is a difficult subject for a
large number of people, and that is why we see so many mathematics videos on youtube. Included are many videos from the now
controversial Khan academy. The common
argument we see is that the definition of mathematics changes as the medium it
is placed in changes.
“YouTube videos, digital photos, MP3s,
PDFs, blog posts, spoken words, and printed text are all different media and
they are all suited for different messages. When you attempt to distribute mathematics through any of these media, it changes the definition of mathematics.”
To read the full post go here http://blog.mrmeyer.com/?p=12782
So
basically the use of technology to explain mathematics has changed its meaning.
I have two questions I am going to propose.
First:
Is redefining mathematics truly hurting people’s capacity, ability, or
willingness to learn?
To answer this
first question let’s look at khan academy. I just looked them up 5 minutes ago, and on their youtube channel they
have 8.3 million channel views and 121,000,000 total upload views. Now according
to the U.S. census bureau in 2010 there were approximately 83 million people
age 3 and older in school. This
“implies” that, there are more views than the number of students in the U.S. Now the total views do not represent the total
number of unique views. It does however show a significantly increased interest
to learn mathematics.
Khan academy isn’t
the only source of videos on mathematics circling the internet. It just seems
to be the most “popular”. Many
individuals and other groups all post their knowledge of mathematics in
different formats.
Second:
If this were true for printed text, how did the printing of the very influential
“liber abaci” in the 1800’s change
its meaning from the original hand
written manuscript?
The use of the
Arabic numerals 0-9 and place value are the universal standards today. Without
the use of new technology and new mediums the Liber Abaci would have not have
half the impact it did.
Did this in anyway hurt students’ ability to learn or understand
mathematics? Or did this make it easier to understand and share this knowledge
with the world.
Now let us look
at today’s technology. The computer and the internet have made a huge impact on
the distribution of knowledge. (Just as the printing press
did when it was invented.) The only difference is now with computers
we can share our knowledge with the world nearly instantly. Mathematics has
always been about analyzing and understanding the world around us. The sharing
of knowledge has never changed that definition. It has only enhanced how many
people are able to use mathematics for whatever they wish to analyze or
understand.
What role do educators, parents, and
students have in education?
Degree holding,
certified educators seem to have or desire to have a complete control over how
students are educated. I agree that
educators who have spent years of their life studying their craft deserve a
certain level of respect. However, we need to ask are they all still living up
to the respect that their “title” deserves, or is the title “all” that accredits
them. ( I am not saying that all
teachers “hide” behind their title. I am just simply saying that it sadly does
happen) Parents and teachers both are missing the most import factor
that controls a students learning. That is the students themselves. Students
learn from each other and from all of their experiences combined, more than they
learn from schools.
When you look at other countries that surpass the U.S. in
math and science scores, most would wonder what they are doing differently. In general U.S. students (k-12) are punished for
discussing, disagreeing, or criticizing problems offered during class. (This is a generalization that does not “always” happen in “all
“classrooms, but it unfortunately does happen)
In Japan, for example, we see a complete opposite practice. The students there are encouraged to discuss
and criticize the material in order to gain a full understanding of all ways to
look at a problem.
To better explain this here is a quote from a case study from the National Institute on Student Achievement, Curriculum, and
Assessment prepared by Angela Wu.
“ While
students look to teachers for comprehension and evaluation in American
classrooms, students look to each other in Japanese whole-class instruction classrooms.
The teacher asks the class to evaluate individual students' solutions to math
problems.”
Group focused
learning is teaching students to teach themselves, and each other. When we look
at this we can wonder, how this relates to the flood of tutorial videos and
other online media for teaching and learning.
The group learning mentality has evolved past the students in one
classroom or even one country learning from each other. It has evolved into
individuals who are not educators, but are more knowledgeable on a subject than
their target audience. These individuals share their knowledge in the best way they
can, to reach as many people who can benefit from it as possible. The individuals that provide their knowledge
for free should be given as much respect as any other educator whether they
just teach the mechanics of a subject or teach the philosophy behind it.
Do Silicon Valley and regular classrooms actually
tell students the same thing?
Rote memorization and mechanical repetition of tasks is
exactly how the “majority” of educators teach mathematics. It is a sad truth,
but it is the truth. (I am sure a lot of
educators would completely disagree with me on this, but even if I get 1000
emails/comments on this that number will still represent the minority of
educators.)
A lot of the individual
video tutorials found on the internet also provide this type of instruction.
The big difference is that Silicon Valley or computer based instruction is available
to everyone at any given time.
“On the one hand, Silicon Valley tells students, "Math
is a series of simple, machine-readable tasks you watch someone else explain
and then perform yourself." Our best classrooms tell students, "Math
is something that requires the best of your senses and reasoning…”
This statement implies that there is a separation between Silicon
Valley and the “…Best classrooms…” Although this may be in part true, the number
of the “best” classrooms is not a big number. I do completely agree with Dan’s last
statement "Math is something that requires the best of your senses
and reasoning…”
Math does require your senses and reasoning. That is why I
feel there should be a prerequisite class on logic and critical thinking prior to
taking any math class pre-algebra and above.
After taking the prerequisites, logic and critical thinking should be
merged into the rest of the mathematics instruction. Additionally, the online resources such as
Khan Academy and others should be used to supplement the limited time teachers
have for instruction in classes. A certain amount of repetition and
memorization is needed in mathematics, but neither approach should be the "only" way
to educate.
Friday, February 10, 2012
Magic Squares: The Math that Drives Them
What is the Math behind Magic Squares?
A magic square is basically just an arithmetic sequence arranged in a special way. What do we know about an arithmetic sequence? An arithmetic sequence is a sequence of numbers each with a common difference. Looking at it a different way, it is a sequence of number by which each number in the sequence is found by adding a specific number to the first number in the sequence. For Example: The sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11....
is a sequence that starts with 1 and each successive number in the sequence is found by adding 1 to the previous number in the sequence . Now let’s say we want to know the sum of the first 9 digits in this sequence. We could just add them all up one at a time, but that generally takes more time. And with larger sequences it would take a really long time. So we will set up a formula.
Looking at a arithmetic sequence algebraically we need to set up some variables. We will denote the starting value with, a, and the common difference with x and each term is n so algebraically an arithmetic sequence looks like this A, (A + X),( A + 2X), (A +3X), (A +4X), ….. (A + Nx),
Where (A + nX) is the nth term in the sequence. sn is the sum of the ne terms
When we wish to know the sum of n terms of the sequence what we are saying algebraically is
sn = a + (a + x) +...+ (a + 2x) + …+ (a + (n-2) x) + (a + (n-1) x)
And in order to reduce this to a simple formula we can work with we will take the above sequence and reverse it and add it to itself.
Sn = a + (a + x) +...+ (a + 2x) + …+ (a + (n-2) x) + (a + (n-1) x)
+ Sn = (a + (n-1) x) + (a + (n-2) x) +…+ (a + 2x) +… + (a + x) + a
2 Sn = (2a + (n-1) x) + (2a + (n-1) x) + …+(2a + (n-1) x) +…+(2a + (n-1) x)
Since we are working with sequences of n terms grouping the last part is as simple as taking
(2a + (n-1) x), and multiplying it by n
2 Sn = n (2a + (n-1) x)
Then when we divide by 2 we have Sn = n (2a + (n-1) x)
2
The resulting equation is close to what we will be using for magic squares.
The only difference is that with
Sn = n (2a + (n-1) x) is used with linear sequences that can be graphed out on a
The only difference is that with
Sn = n (2a + (n-1) x) is used with linear sequences that can be graphed out on a
2
number line. In order to modify this for working with magic squares we simply square the n Inside the parenthesis ()
which changes our equation to Sn = n (2a + (n2-1) x) We do this
which changes our equation to Sn = n (2a + (n2-1) x) We do this
2
because (n-1) is used to represent last term and in magic squares the number of terms is the dimension squared so the last term would be (n2-1).
Magic squares: basic construction method
How to construct a 3x3 magic square
In this section we will be constructing the basic magic square with the dimension 3x3 starting value 1 and common difference 1. If you do not know what a magic square is please refer to the Magic Squares: Introduction section. It is also important to note that this method works with all magic squares that have an odddimension. i.e. 5x5 7x7 9x9.......
1. ) First we will begin with an empty 3x3 array.
2.) Next we place the starting value 1 in the middle of the top row.
3.) Now we move right one space and up one space,
but as we can see highlighted in yellow this places the 2
outside the bounds of the 3x3 square.When this happens we
simply bring the 2 down to the bottom square of the column it is positioned over.
4.) In this step we start with the 2 and once again we go right
one space and up one space. And once again this leaves us
out side the bounds of the 3x3 square so we place the 3 at the
beginning of the row it is outside of.
5.) Here we start with the 3 and once again move right
one space and up one space, but this time it puts us in an
occupied space. when that happens we simply place the 4
underneath the 3.
6.) In this step we start with the 4 and again move right one
space and up one space. This space is within the bounds of the
square and unoccupied so we can simply leave the 5 here.
7. ) Here we start with the 5 and go one space right and one
space up and as we can see we can once again simply just
place the 6 in this unoccupied space
8.) This time when we move right one space and up one
space. we are not only outside the bounds of the square
but we are also on a diagonal In case this happens we
place the 7 underneath the 6.
9.) Here we start with the 7 and move right one space
and up one space. Here we are again out side the bounds
of the square so we simply take the 8 and place it at the
beginning of the row it is beside.
10.) now in the final step we only have one space left where we could go ahead and place the 9 there how ever I am still going to illustrate that the pattern still applies when there is only one space. so we start with the 8 move right one space and up one space. and again we are out side the bounds of the square, so we will move the 9 to the bottom of the column it is over.
Next in the series we will be looking deeper into the math behind these squares.
Magic Squares: introduction
What are magic Squares ?
Magic squares are an arrangement of numbers in a grid of various dimensions to where each row, column, and diagonal will sum up to the same number. The grid they are placed in is generally a N x N array split into N² cells.For example: a 3 x 3 square will have 9 cells meaning there will be 9 numbers in the square.
Here is an example of a 3 x 3 magic square.
Here is an example of a 3 x 3 magic square.

Top Row : 4 + 9 + 2 = 15
Middle Row: 3 + 5 + 7 = 15
Bottom Row: 8 + 1 + 6 = 15
Left Column: 4 + 3 + 8 = 15
Middle Column: 9 + 5 + 1 = 15
Right column: 2 + 7 + 6 = 15
First Diagonal 4 + 5 + 6 = 15
Second Diagonal 2 + 5 + 8 = 15
Magic squares are an exciting study of number arrangements. Mathematicians have been fascinated by magic squares for centuries.They can be both fun and educational. Magic squares have a deep relation to a branch of mathematics known as combinatorics. However, most just use them for entertainment.
A birthday trick for magic squares
All Magic squares have a few basic components that you can use to create one. First you need a starting value, that is the lowest number that will be in the square. Second you need to know the common difference between the numbers in the square. For example in the above square it contains all of the numbers 1, 2, 3 , 4 , 5 , 6, 7 ,8 , 9 each number in the series is obtained by adding 1 to the previous. so the common difference between terms is 1 The third component of a magic square is the dimension. For Example. The above square has 3 rows and 3 columns so its dimension is 3 x 3.
Now for our birthday trick we will restrict the dimension to a 3 x 3. You may also want to keep a copy of the above square so you can see the order you put the numbers into, or you can save it and print it off to use in the trick..
(there is a method for constructing magic squares without using an already created one as a reference but ill include that in my continuation of the series on magic squares)
(there is a method for constructing magic squares without using an already created one as a reference but ill include that in my continuation of the series on magic squares)
- Now what you will do is ask a person for the month and year they were born, or use your own birthday.You use the last 2 digits of the year they were born for simplicity(or if you are really comfortable with your mental math skills you could use the whole year)
- You take those 2 digits and use it as the starting value and you use the numerical value for the month as the common difference.
- And in your head you multiply the month times 4 and add it to the 2 digit year
- you write down the result where they cant see you writing
- then you then put the piece of paper with the number on it in your pocket
- you then use the year and month of their birth to construct a magic square.
- once constructed you show them that every row column and diagonal all have the same sum
- next you have them divide that sum by 3 and tell you the answer
- you then pull the piece of paper out of your pocket and "magically" it is the same number
Ill show an example of this using Benjamin Franklin's birth day 01/17/1706
- 01/17/1706
- .starting value =06 common difference=1
- 4 x the month 1 + 06 = 4 + 6 = 10 (here i will multiply times 3 so i can omit step 8 since) 10 x 3 = 30
- 30 ( not actually writing down because this is an example)
- also skipping this step because its an example
Middle Row: 8 + 10 + 12 = 30
Bottom Row: 13 +6 + 11 =30
Left Column: 9 +8 + 13 =30
Middle Column: 14 + 10 + 6 =30
Right column: 7 + 12 + 11 = 30
First Diagonal 9+ 10 + 11 = 30
Second Diagonal 7 +10 + 11 = 30
As you can see the magic constant is the same number we got in step 3
Here is a side by side comparison of the square from the example and the basic square I placed at the top so you can see how you can use the basic square to construct a square for the trick.
The next part in the series will be how to construct a magic square given any starting value,common difference, and dimension without using the basic square as a template. I will be posting this in about 12 hours so be sure to check back with us.
Subscribe to:
Posts (Atom)










