We are moving our website

I would like to think everyone who has been following this blog. We have moved to a new platform and a new url @ http://www.mathjourney.com/   please join us there. Thank you again for following us and we hope to see you at our new Math Journey

Inversion

Inversion is a process of working backwards, or inverting operations to solve a problem. Example of inverse operations are addition and subtraction. They are each an inverse of the other. Multiplication and division are inverses. Just as you can work backwards to check a solution to a problem you can work through inversion to find many ways to solve problems from the mundane to the extremely complex.



We can use inversion to add two numbers without adding. In, fact we can use it to add through the use of subtraction.  For example: we can add 3 + 5 by subtraction. First we will subtract 3 from 10 to get 7 then from 7 we well subtract the next number 5 to get 2. We can then subtract 2 from 10 again to get 8.



Now this seems an incredibly long way to add two numbers together. Yet, the importance is not in the specific inversion itself. It is in the way of thinking that it promotes. The ability to conceive of a new way of approaching a problem can often lead to a more profound discovery. It could lead you into finding a way to solve entire groups of problems.



It is a simple concept, work backwards. Look at the data and work backwards to determine the source.
An example can be found in inverse scattering problems. These problems look at the scattering to determine the source, or likely causal factors. Such as in sonar technologies. You look at the variations in the sound wave echos to locate objects.



The inverse scattering problem solving technique is also used in medicine. The Positron emission tomography (PET) scan uses the detection of photon bursts from the beta decay of radioisotopes.
Then working to generate an image of the targeted tissue from the scattered data.



It it is based on the category of problems called inverse problems. In these problems the likely source is the unknown, and only through inversion can you find trace back to the source. It is probably the most important class of problems, with this most important process of solving them.

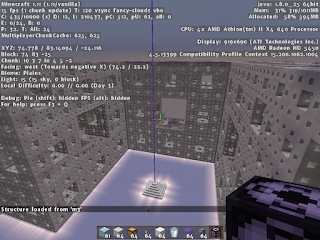
5th Iteration Minecraft Mighty Menger Sponge!!!!!!!!!!!!!!!

In an earlier post I created a 4^th iteration 160,00 block Menger Cube in minecraft. After I discovered the newly added structure block I was able to construct the 5^th iteration 3,200,000 block version.

After I cleared out a large enough area all the way down to bedrock I began construction.

Here is the bottom section with 5, 4th iteration menger cubes

The 32x32x32 limit of the structure block meant that I had to use 3rd iteration 8,000 block menger cubes Menger cubes to construct this because the 4th iteration was more than the 32 cubed or 32,768 limit.

An fun side note is that I constructed this with x = 0, z  =  0 at the very center.

With the bottom section of 8, 4th iteration Menger cubes finished I it was time to do the second row of 4,

And the beginning of the top row of 8, 4th iterations menger cubes

From the above picture you can see the outline of the structure block for the 3rd iteration Menger cube. It takes 20 of the 3rd iteration to make a 4th iteration so for each of the 20, 4th iteration cubes I had place the structure block 20 times. That is still a huge drop from having to place each of the 3.2 million cubes.


If you can't make out the y coordinates below this structure goes from y = 0 to just under the minecraft build height limit. What this means is that the 6th generation is not gonna happen in minecraft unless that limit is changed.

Another side note a quick way to clear an area using the structure block is to save a 32x32x32 area of just air then use the structure blocks in the area you need to clear. You could also use the /fill command to fill an area with air but I like the structure block approach.


Here is a few shots of the finished product a megalith of 3.2 million blocks!!!!!!

And here is a few shots of me starting to decorate the inside.

Multiplication with positional notation and the distributive property

In this post we will be learning how to use positional notation to perform multiplication.

If you need a review on positional notation please refer to my previous post on this subject.
Positional Notation

To refresh on what positional notation looks like we will write the number 235 with positional notation.

With a smaller example we can see if this allows us to learn something new about multiplication.

So to multiply 32 and 24 we will first write these two numbers into positional notation.

Does this look familiar? If we replace the 10 with x and since 10⁰ = 1 we will

 replace it to and then we have:.

To put into a more familiar form:

(3x + 2)(2x + 4)

With our number in this form we can now use basic algebra.

From distributive property.

a(b+c)

=

(ab)

+

(ac)

We can now multiply this out using what is sometimes referred to as the foil method *(First Outer Inner Last)

Now if we substitute the 10 back in for x

To see how this works scaled up we will multiply 3259 and 1564

And again we can put this into the familiar form:Now again to replace the 10 with x and since 1(x) is just x we remove the 1 in the second number:

Now we gather like terms:

If we put the 10 back in for x then multiply we will get

And here is our answer using positional notation and distributive property to multiply two numbers. 

5,097,076

Minecraft 4th iteration Menger Sponge

Minecraft Menger sponge (Menger Universal Curve) :

The Menger sponge is a 3 dimensional cube that models the Sierpinski carpet. The Sierpinski carpet is a fractal generalization of the Cantor set.

The Sierpinski carpet is a 2 dimensional figure starting with a square and then subdividing into 9 sections. You then remove the center section.

  

The next step is to take the remaining 8 sections and repeat the process for each one.

After that you are left with an image where the middle section is missing from each of the 8 subsections of the original figure. You then take each of those subsections and repeat the process again. This will leave you with this figure:

You can then repeat the process again....

An amazing property of the Sierpinski carpet is that as the number of iterations of this process approaches infinity the area will approach 0

When this process is moved up into 3 dimensions you construct a Sierpinski sponge. The Menger cube is slight alteration of the Sierpinski sponge.

The Menger sponge has a similar amazing property that as the iterations approach infinity the Surface area approaches infinity and the Volume approaches 0..  

I created a 4 iteration Menger sponge in Minecraft, starting with a 3X3X3cube.

Then I removed the center block from each of the 6 faces.

I Then cloned this cube using the Minecraft /clone command to get to 20 cubes arranged to show the next iteration of the Menger sponge.

I then cloned that cube to make 20 more copies to construct the next iteration.

At this point I will note that for the Menger sponge the number of cubes (or in this case blocks) is given by the formula (Number of blocks) N = 20ⁿ where n is the number of iterations and the above cube is iteration 3. which is N = 20³ = 8000 blocks.

For the final project I decided to move over into my realms server and construct a 4 iteration Menger cube with N = 20⁴ = 160,000 blocks...!!!!

The controversy with common core:

The controversy with common core:

     Math has become a new phobia among youth and current parents. It has many wearing math illiteracy as a badge of honor. The problem began with adults experiencing negativity at a young age toward the subject. It was often taught in very rigid and mechanical tone. The rigidity is where the problem we face today finds its roots. Math was drilled into our heads with the idea that there is only one way to do things, and anything else leads to lower grades. Many teachers were strictly against alternative methods, and led to an ingrained aversion to the subject for their students.

     Other issues include the teaching methods themselves, as well as the lack of guidance for students who may take longer to grasp the subject. In the interest of time, and testing, the teachers are encouraged to cover large amounts of material in a short amount of time. These factors in combination are what has resulted in the attitude toward math that parents possess today. This attitude is also being passed on to their children, by encouraging an avoidance of mathematics. The parents own aversion and lack of proper education in mathematics makes it difficult to understand the material their children are bringing home. The new common core standards and teaching tools are incredibly different from what many of these parents are familiar with.

      

      Currently students are being introduced new concepts for learning math with the development of common core. Altering how things are done, can be beneficial to finding better teaching options. Sure many of these methods are breaking from tradition, but as with all things we are learning. Which forces us to integrate new information and approaches to teaching. Parents and educators all need to stay aware of this. As we learn and grow intellectually, knowledge must force us to change. However, this change conflicts with the fact that the parents of these children are unable to help them to better their skills in these areas. Here we see the roots of the problem. The parents were not taught by common core standards, and therefore cannot aid their children until first learning the methods themselves.

     If parents or teachers see common core standards as a problem maybe schools could host a week long open seminar on what is actually going to be taught and how it is implemented. The schools could have qualified instructors in the common core standards come and talk with parents and teachers. They could even teach some of the new math strategies to the parents so they can be better informed on how to help their children adapt to the new material.

     Given the chance to come to understand the common core math standards could help change the way some respond to them. I understand the problems many people have with common core math. Seeing a drop in test scores with new standards being put into place is a shock, but when you look into it you see it is not the problem with the tests, it is us. We are failing our children. The common core math standards are well informed and vetted by leaders in the stem fields. And these are the things our children need to learn to remain competitive with their peers around the globe.

The largest prime

The largest prime number ever seen by humankind was found on January 7, 2016.  It weighs in at  22,338,618 digits in length. It is what is known as a Mersenne prime (2^74,207,281-1).  Mersenne primes are a group of prime numbers of the form 2ⁿ -1 where n is  is assumed to be prime. This is a fascinating find. Prime numbers are the "building blocks" of all other numbers.  Their unique nature has led many number theorists and math enthusiasts to study them in great detail. Although they are used heavily in cryptography, the latest find is far too large to be used in any encryption schemes to date. But as computation theory evolves and computer architectures become more sophisticated these extremely large primes may find their place.